확률 분포

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 확률 분포의 분류
- 3.1. 이산 확률 분포
- 3.2. 연속 확률 분포
  - 3.2.1. 절대 연속 분포
  - 3.2.2. 특이 분포
4. 대표적인 확률 분포
5. 확률 분포의 활용
6. 변수 변환
- 6.1. 확률 밀도 함수의 변수 변환 공식
- 6.2. 확률 변수 합의 확률 분포
7. 확률 모델
8. 난수 생성
9. 일반적인 확률 분포와 응용
10. 적합
참조

1. 개요

확률 분포는 확률 변수가 특정 값을 가질 확률을 나타내는 함수이다. 확률 질량 함수, 누적 분포 함수 등 다양한 형태로 표현되며, 입력 공간과 실수 범위를 갖는 확률 함수로 정의할 수 있다. 확률 분포는 콜모고로프 공리를 만족해야 하며, 이산 확률 분포와 연속 확률 분포로 분류된다. 이산 확률 분포는 확률 변수가 이산적인 값을 가질 때, 연속 확률 분포는 연속적인 값을 가질 때 사용된다. 확률 분포는 확률 계산, 기댓값 계산, 분산 계산 등에 활용되며, 변수 변환을 통해 새로운 확률 분포를 유도할 수 있다. 또한, 퍼콜레이션, 랜덤 워크, 무한 입자계 등 다양한 확률 모델에서 활용되며, 난수 생성, 데이터 적합 등 통계적 모델링에도 중요한 역할을 한다.

더 읽어볼만한 페이지

확률분포 - 베르누이 분포
베르누이 분포는 성공 확률 p를 가지며, 단 한 번의 시행에서 성공 또는 실패 두 가지 결과를 나타내는 이산 확률 분포로, 기댓값은 p, 분산은 p(1-p)이며 다른 여러 확률 분포와 관련되어 불확실성과 정보량을 측정할 수 있다.
확률분포 - 로그 정규 분포
로그 정규 분포는 확률 변수 X의 로그가 정규 분포를 따르며, 양의 실수 값을 갖고 평균 μ와 표준 편차 σ를 매개변수로 갖는 확률 분포이다.

확률 분포

2. 정의

확률 분포는 표본 공간의 부분 집합인 사건의 확률에 대한 수학적 설명이다. 표본 공간은 관찰되는 임의 현상의 모든 가능한 결과의 집합이다. 예를 들어, 동전 던지기의 표본 공간은 {앞면, 뒷면}이 될 수 있다.

확률 변수의 특정 경우에 대한 확률 분포를 정의하기 위해, '''이산''' 및 '''절대 연속''' 확률 변수를 구별한다. 이산 확률 변수의 경우, 각 가능한 결과에 확률을 할당하는 확률 질량 함수를 지정한다. 예를 들어, 공정한 주사위를 던질 때 주사위의 점 수에 해당하는 여섯 개의 숫자는 각각 $\ \tfrac{1}{6} ~$ 의 확률을 갖는다.

반대로, 확률 변수가 연속체에서 값을 취할 때, 개별 결과에는 확률 0이 할당된다. 이러한 '''연속 확률 변수'''의 경우, 무한히 많은 결과를 포함하는 사건만 0보다 큰 확률을 갖는다. 예를 들어, 슈퍼마켓에서 햄 조각의 무게를 측정할 때, 정확히 500g의 무게가 나갈 확률은 0이다.

절대 연속 확률 분포는 확률 밀도 함수로 설명할 수 있다. 주어진 간격에 결과가 있을 확률은 해당 간격에 대한 확률 밀도 함수를 적분하여 계산할 수 있다.^[7] 또는 누적 분포 함수를 사용할 수 있다. 이는 확률 변수가 주어진 값보다 크지 않을 확률을 설명한다. 누적 분포 함수는 확률 밀도 함수 아래의 면적이다.^[4]

확률 함수 $P\colon \mathcal{A} \to \Reals$ 는 다음의 모든 콜모고로프 공리를 만족하는 경우에만 확률 분포를 특징짓는다.

# $P(X \in E) \ge 0 \; \forall E \in \mathcal{A}$ , 확률은 음수가 아님

# $P(X \in E) \le 1 \; \forall E \in \mathcal{A}$ , 확률은 1을 초과하지 않음

# $P(X \in \bigcup_{i} E_i ) = \sum_i P(X \in E_i)$ , 모든 가산 분리 집합족 $\{ E_i \}$ 에 대해 성립

확률 분포는 일반적으로 '''이산 확률 분포'''와 '''절대적으로 연속적인 확률 분포''' 두 가지 종류로 나뉜다. 이산 확률 분포는 가능한 결과 집합이 이산적인 경우에 적용되며, 확률 질량 함수로 표현된다. 절대적으로 연속적인 확률 분포는 가능한 결과 집합이 연속적인 범위의 값을 가질 수 있는 경우에 적용되며, 확률 밀도 함수로 설명된다. 정규 분포는 대표적인 절대적으로 연속적인 확률 분포이다.

확률 함수 외에도, 누적 분포 함수, 확률 질량 함수 및 확률 밀도 함수, 적률생성함수, 특성 함수도 확률 분포를 식별하는 데 사용된다.

2. 1. 확률 분포

확률 분포는 측도론적 확률론의 형식화에서, 확률 공간에서 가측 공간으로의 가측 함수로 정의되는 확률 변수에 의해 결정되는 확률 측도이다.^[1] 확률 변수 X의 확률 분포는 X의 푸시포워드 측도로 정의된다.

예를 들어, "주사위 2개를 던졌을 때의 눈의 합"은 확률 변수이며, 이 확률 변수에 대한 분포는 다음 표와 같다.

가 취하는 값	2	3	4	5	6	7	8	9	10	11	12
확률	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

이는 이산 확률 변수의 경우, 확률 분포가 확률 변수의 값에 그 확률(확률 질량 함수)을 대응시키는 함수임을 보여준다. 그러나, "다음에 전화가 걸려올 때까지의 시간"과 같은 연속형 확률 변수의 경우에는 확률 변수 값에서의 확률이 모두 0이 되어, 확률 분포를 확률 질량 함수로 나타낼 수 없다.

"다음에 전화가 걸려올 때까지의 시간"을 확률 변수 X로 설정하고, 그 분포가 다음과 같다고 가정한다.

X가 취하는 범위	1시간 이내	1–2시간 후	2–3시간 후	3–4시간 후	4시간 이상
확률	1/2	1/4	1/8	1/16	1/16

이 경우, 확률은 모든 연속 구간에서 계산되어야 한다. 다음 전화가 a - b 시간 후에 걸려올 확률은 다음 식으로 나타낼 수 있다.

: $P(a$

누적 분포 함수 F_X(t)를 정의하면,

: $F_X (t)=P(X \leq t)= \begin{cases}1- \left( \frac{1}{2} \right)^t, &t \geq 0 \\0, &t<0\end{cases}$

: $P(a$

와 같이 일변수 함수로 분포를 표현할 수 있다. 또한, F_X의 도함수 f_X는 확률 밀도 함수라고 불리며, 확률은 적분을 이용하여 다음과 같이 표현할 수 있다.

: $P(a$

일반적으로 연속 값을 취하는 확률 변수의 분포는 초등 함수로 표현 가능한 확률 밀도 함수를 이용하여 기술된다.

공리주의적인 확률론에서는 확률 분포를 d차원 유클리드 공간상의 확률 측도로 정의한다. 이는 확률 변수의 값이 특정 집합에 속할 확률을 나타내는 함수가 된다.

확률 분포는 d차원 유클리드 공간 등에서 정의된 확률 측도를 의미하며, 확률 측도와 달리 분포의 형태를 시각적으로 표현할 수 있다는 특징이 있다.

확률 변수의 분포를 고려하는 것은 해당 변수만을 확률론적 논의의 대상으로 삼고자 할 때 유용하다. 예를 들어, 확률 변수의 특정 값, 기댓값, 분산 등은 변수의 분포를 통해 계산할 수 있다. 그러나 분포를 통해 변수 간의 관련성은 파악하기 어렵다. 예를 들어, 두 확률 변수 X와 Y의 분포가 각각 P_X와 P_Y로 주어져도, 두 변수의 관련성을 알 수 없어 X + Y의 값, 곱 XY의 기댓값, X + Y의 분산 등을 계산할 수 없다. 이러한 값을 계산하려면 X와 Y의 결합 확률 분포 P_X,Y가 필요하다.

자주 사용되는 확률 분포는 각각의 이름과 특징을 가지며, 이를 통해 확률 변수에 대한 연구 결과를 활용할 수 있다. 예를 들어, 확률 변수가 평균 0, 분산 1의 정규 분포를 따르면, 변수가 2 이상의 값을 가질 확률은 2.28%이다.

1차원 확률 분포는 가측 공간 $( \mathbb{R}, \mathcal{B} ( \mathbb{R} ))$ 위에서 정의된 확률 측도를, d차원 확률 분포는 $( \mathbb{R}^d, \mathcal{B} ( \mathbb{R}^d ))$ 위에서 정의된 확률 측도를 의미한다. 여기서 $\mathcal{B} ( \mathbb{R}^d )$ 는 $\mathbb{R}^d$ 위의 보렐 집합족이다.

실수값 확률 변수 X의 확률 분포 $P_X : \mathcal{B} ( \mathbb{R} ) \to [0,1]$ 는

: $P_X (A) = P(X \in A),\ \ \ A \in \mathcal{B} ( \mathbb{R} )$

로 정의되며, P_X는 확률 측도(상측도)이다.

마찬가지로 $\mathbb{R}^d$ 값 확률 변수 X의 확률 분포 $P_X : \mathcal{B} ( \mathbb{R}^d ) \to [0,1]$ 는

: $P_X (A) = P(X \in A),\ \ \ A \in \mathcal{B} ( \mathbb{R}^d )$

로 정의되는 확률 측도이다.

확률 변수 X의 확률 분포가 μ일 때, X는 μ를 따르는 확률 변수라고 하며, X ~ μ로 표기한다.^[35] 예를 들어, "X는 평균 0, 분산 1의 정규 분포를 따른다"는

: $X \sim N(0,1)$

과 같이 표기한다.

2개 이상의 변수에 대한 확률 분포는 다차원 확률 분포라고 하며, 2변수의 확률 분포는 이차원 확률 분포라고 한다.

2. 2. 확률 변수의 확률 분포

확률 변수의 확률 분포는 확률 변수가 특정 값을 가질 확률을 나타내는 함수이다. 이산 확률 변수의 경우, 가능한 값의 개수가 정해져 있으며(가산), 확률 질량 함수를 통해 각 값에 대한 확률을 표현한다. 예를 들어, 주사위를 던졌을 때 나오는 숫자는 이산 확률 변수이며, 각 숫자가 나올 확률은 1/6로, 확률 질량 함수로 나타낼 수 있다.^[7]

연속 확률 변수의 경우에는 가능한 값이 연속적인 범위로 주어지며, 확률 밀도 함수를 사용하여 분포를 표현한다. 예를 들어, 특정 지역의 온도 변화는 연속 확률 변수이며, 확률 밀도 함수를 통해 특정 온도 범위에 속할 확률을 계산할 수 있다.^[7] 누적 분포 함수는 확률 변수가 특정 값보다 작거나 같을 확률을 나타내며, 확률 밀도 함수를 적분하여 구할 수 있다.^[4]

예를 들어, "주사위 2개를 던졌을 때 눈의 합"은 확률 변수이다. 이 확률 변수에 대한 분포는 다음과 같이 표로 나타낼 수 있다.

확률 변수가 취하는 값	2	3	4	5	6	7	8	9	10	11	12
확률

이처럼 이산 확률 변수의 경우, 확률 분포는 확률 변수의 값에 그 확률(확률 질량)을 대응시키는 함수(확률 질량 함수)로 나타낼 수 있다.

"다음에 전화가 걸려올 때까지의 시간"과 같은 연속형 확률 변수의 경우, 특정 시점에 전화가 올 확률은 0이므로, 확률 분포를 확률 질량 함수로 나타낼 수 없다. 대신, 특정 시간 범위 안에 전화가 올 확률을 다음과 같이 표로 나타낼 수 있다.

확률 변수가 취하는 범위	1시간 이내	1–2시간 후	2–3시간 후	3–4시간 후	4시간 이상
확률

이 경우 누적 분포 함수와 확률 밀도 함수를 이용하여 확률 분포를 나타낼 수 있다.

2. 3. 누적 분포 함수

실수 값 확률 변수의 '''누적 분포 함수''' (cumulative distribution function|CDF^영어) 또는 1차원 확률 분포의 누적 분포 함수는

:

F_X (x) = P(X \leq x) = P_X ((-\infty, x])

로 주어지는 함수 를 말한다. 누적을 생략하여 '''분포 함수''' (distribution function^영어)라고도 한다.

누적 분포 함수는 정의에 따라 우(右)연속이지만, 좌(左)연속일 필요는 없다. 누적 분포 함수가 연속인 (좌연속이기도 한) 확률 분포를 '''연속 확률 분포'''라고 한다. 누적 분포 함수가 취하는 값이 고작 가산(可算)개인 확률 분포를 '''이산 확률 분포'''라고 한다.^[4]

2. 4. 확률 밀도 함수

확률 분포 ''P''가 절대 연속이면, 어떤 가측 함수 가 존재하여, 확률 분포는

:

P(X \in A) = P_X (A) = \int_A f_X (x) \, dx

로 표현된다 (라돈-니코딤 정리).^[18] 는 의 라돈-니코딤 미분이며, 영집합을 제외하고 유일하다. 를 연속형 확률 변수 의 '''확률 밀도 함수''' (probability density function, PDF)라고 한다.^[19]^[20]

확률 분포 가 절대 연속이라는 것은, 임의의 (르베그 측도에 관한) 영집합 에 대하여,

:

P_X (N) = 0

이 성립하는 것으로 정의된다. 이는 측도의 절대 연속성과 같다. 이때 연속 확률 분포이다.

특히 가 구간인 경우에는

:

P(a < X < b) = P(a \leq X < b) = P(a < X \leq b) = P(a \leq X \leq b) = \int_a^b f_X(x) \, dx

가 된다. 구간의 양 끝점은 포함하든 포함하지 않든 확률은 같다.

2. 5. 확률 질량 함수

probability mass function^영어는 이산 확률 분포에서 특정 값에 대한 확률을 나타내는 함수이다. 이산 확률 변수가 취할 수 있는 값의 집합을

S = \{x_1, x_2, \dots \}

라고 하면, 확률 질량 함수는 다음과 같이 정의된다.

:

f_X (x_i) = P(X = x_i) = P_X(\{x_i\})

즉, 확률 변수

X

가 특정 값

x_i

를 취할 확률을 나타낸다.

예를 들어, 주사위 2개를 던졌을 때 눈의 합에 대한 확률 분포는 다음과 같이 표로 나타낼 수 있다.

$X$ 가 취하는 값	2	3	4	5	6	7	8	9	10	11	12
$P(X$ 의 값이 $n$ 을 취함 $)$

이 표는 확률 질량 함수를 나타낸다. 예를 들어, 주사위 눈의 합이 7일 확률은 $\tfrac{6}{36}$ 이다.

한국어에서는 확률 질량 함수를 '''확률 함수'''로 줄여서 말하기도 하지만, 영어의 probability function^영어은 의미가 모호한 단어로 간주된다.

2. 6. 다변량 확률 분포

둘 이상의 변수에 대한 확률 분포를 다변량 분포라고 한다. 일변량 분포는 단일 확률 변수가 다양한 값을 가질 확률을 제공하는 반면, 다변량 분포(결합 확률 분포)는 여러 확률 변수들의 목록인 확률 벡터가 다양한 값의 조합을 가질 확률을 제공한다.^[34] 2변수의 확률 분포를 이차원 확률 분포라고도 한다.^[1] 흔히 사용되는 다변량 분포로는 다변량 정규 분포가 있다.^[34]

2. 6. 1. 결합 분포

2개 이상의 변수 쌍의 확률 분포를 '''결합 분포'''(joint distribution) 또는 결합 확률 분포라고 한다.^[1]^[2]

2. 6. 2. 주변 분포

결합 분포에서 각 변수의 분포만 추출한 것을 주변 확률 분포라고 한다. 일본 산업 규격에서는 "k차원 확률 변수의 부분 집합인 k - 1 변수의 결합 분포"로 정의하고 있다.^[1]

3. 확률 분포의 분류

확률 분포는 확률 변수의 값에 따라 크게 두 가지로 나뉜다.

확률 변수가 이산적인 값을 가지면(예: 주사위 눈의 숫자) 이산 확률 분포를 따른다. 이산 확률 분포는 확률 질량 함수로 표현한다.

반면, 확률 변수가 연속적인 값을 가지면(예: 특정 지점 통행인의 체중) 연속 확률 분포를 따른다. 연속 확률 분포는 확률 밀도 함수를 사용하여 표현한다.

연속 확률 분포는 다시 누적 분포 함수의 연속성에 따라 세분화된다.

절대 연속 분포: 누적 분포 함수가 절대 연속 함수인 경우이다.
특이 분포: 누적 분포 함수가 연속이지만 절대 연속은 아닌 확률 분포이다. 칸토어 분포가 특이 분포의 예시이다.^[21]

흔히 사용되는 확률 분포는 이산 확률 분포와 절대 연속 확률 분포이다.

3. 1. 이산 확률 분포

이산 확률 분포(discrete probability distribution^영어)는 확률 변수가 가질 수 있는 값의 개수가 가산 개일 때, 이산 확률 변수가 가지는 확률 분포를 의미한다. 이산 확률 분포는 확률 질량 함수를 통해 표현 가능하며, 누적 분포 함수로 표현할 경우 그 함수는 비약적 불연속으로만 증가한다.^[7]

자주 사용되는 이산 확률 분포에는 다음과 같은 예가 있다.

분포	설명
이산균등분포	모든 가능한 값에 대해 동일한 확률을 가지는 분포
푸아송 분포	일정 시간 동안 발생하는 사건의 횟수를 나타내는 분포
베르누이 분포	성공 또는 실패의 두 가지 결과만 가지는 실험의 분포 (예: 동전 던지기)
기하 분포	첫 번째 성공이 나타날 때까지의 시행 횟수를 나타내는 분포
초기하 분포	비복원 추출에서 특정 속성을 가진 표본의 개수를 나타내는 분포
이항 분포	독립적인 베르누이 시행에서 성공 횟수를 나타내는 분포
음이항 분포	특정 횟수의 성공이 나타날 때까지의 시행 횟수를 나타내는 분포
다항 분포	여러 범주에 대한 이항 분포의 일반화

이산 확률 분포는 디랙 델타 함수의 확률 분포인 결정론적 확률 변수로 표현될 수도 있다.^[17]

3. 2. 연속 확률 분포

연속 확률 분포는 확률 밀도 함수를 이용해 분포를 표현할 수 있는 경우를 의미한다. 연속 확률 분포를 가지는 확률변수는 '''연속 확률 변수'''라고 부른다.

확률 변수가 연속적인 값을 가질 때, 개별 결과에는 관례적으로 확률 0이 할당된다. 이러한 연속 확률 변수의 경우, 무한히 많은 결과를 포함하는 사건(예: 간격)에만 0보다 큰 확률이 주어진다.

예를 들어, 슈퍼마켓에서 햄 조각의 무게를 측정하고 저울이 매우 정밀하다고 가정할 때, 정확히 500g이 될 확률은 0이다. 그러나 햄 포장이 490g에서 510g 사이일 확률은 98% 이상이라는 품질 관리 요구 사항은 충족할 수 있다.

자주 사용되는 연속 확률 분포에는 다음과 같은 예가 있다.

3. 2. 1. 절대 연속 분포

'''절대 연속 확률 분포'''는 확률 밀도 함수를 갖는 확률 분포이다. 확률 밀도 함수는 주어진 표본 공간에서 임의의 표본(또는 점)에서의 값이, 확률 변수의 값이 해당 표본과 같을 상대적인 가능성을 제공하는 함수이다.^[7] 실수 확률 변수

X

가 함수

f: \Reals \to [0, \infty]

를 갖는다면, 각 구간

I = [a,b] \subset \mathbb{R}

에 대해

X

가

I

에 속할 확률은

I

에 대한

f

의 적분으로 주어진다.^[19]^[20]

:

P\left(a \le X \le b \right) = \int_a^b f(x) \, dx .

특히,

X

가 단일 값

a

를 가질 확률(즉,

a \le X \le a

)은 0이다. 왜냐하면 위아래 한계가 일치하는 적분은 항상 0과 같기 때문이다.

절대 연속 확률 분포는 누적 분포 함수가 절대 연속 함수인 분포이다.^[21] 이 경우, 누적 분포 함수

F

는 다음과 같은 형태를 갖는다.

:

F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\,dt

여기서

f

는 분포

P

에 대한 확률 변수

X

의 밀도이다.

절대 연속 확률 변수는 확률 분포가 절대 연속인 확률 변수이다.

정규 분포, 균등 분포, 카이제곱 분포 등은 절대 연속 확률 분포의 예시이다.

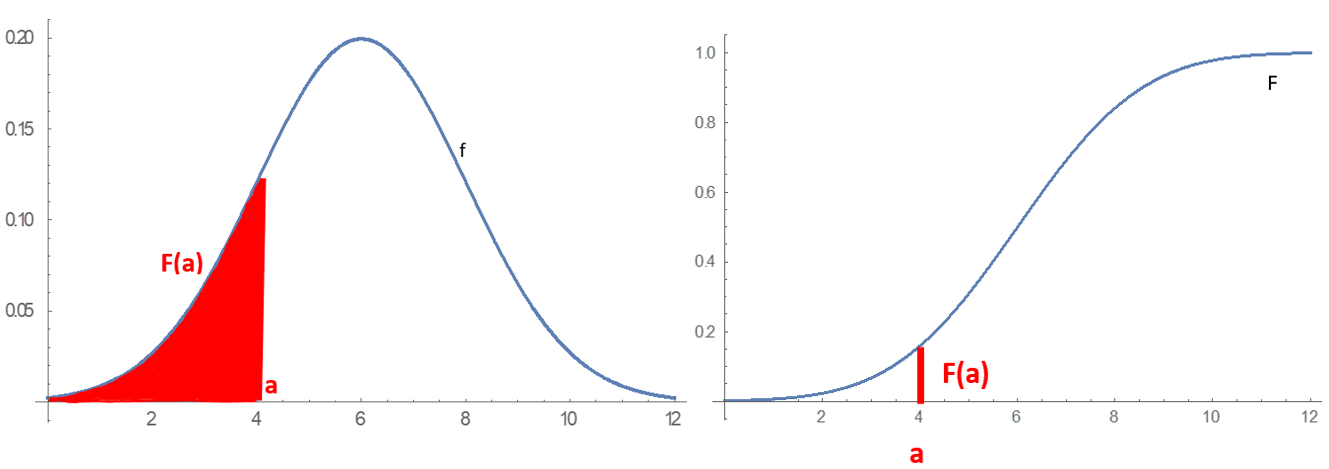
그림 1: 왼쪽 그래프는 확률 밀도 함수를 보여준다. 오른쪽 그래프는 누적 분포 함수를 보여준다. 누적 분포에서 의 값은 지점까지의 확률 밀도 곡선 아래의 면적과 같다.

확률 밀도 함수는 주어진 값의 무한소 확률을 설명하고, 주어진 간격에 결과가 있을 확률은 해당 간격에 대한 확률 밀도 함수를 적분하여 계산할 수 있다.^[7] 누적 분포 함수는 확률 변수가 주어진 값보다 크지 않을 확률(즉,

x

에 대한

\mathcal{P}(X < x)

)을 설명한다. 누적 분포 함수는 그림 1에 표시된 것처럼

-\infty

에서

x

까지의 확률 밀도 함수 아래의 면적이다.^[4]

3. 2. 2. 특이 분포

누적 분포 함수가 연속이지만 절대 연속은 아닌 확률 분포이다. 특이 분포는 이산 확률 분포도 절대 연속 확률 분포도 아니며, 이 둘의 혼합도 아니고 확률 밀도 함수를 갖지 않는다. 칸토어 분포가 특이 분포의 예시이다.^[21]

4. 대표적인 확률 분포

확률 분포는 확률 변수가 특정한 값을 가질 확률을 나타내는 함수이다. 크게 이산 확률 분포와 연속 확률 분포로 나눌 수 있다.

이산 확률 분포: 확률 변수가 가질 수 있는 값이 유한하거나 셀 수 있는 경우의 분포이다. 확률 질량 함수로 표현된다.
연속 확률 분포: 확률 변수가 실수와 같이 연속적인 값을 가질 수 있는 경우의 분포이다. 확률 밀도 함수로 표현된다.

연속 확률 변수의 경우, 특정 값에서의 확률은 0이지만, 특정 구간에 속할 확률은 0보다 클 수 있다. 절대 연속 확률 분포는 확률 밀도 함수로 설명되며, 주어진 구간에 대한 확률은 확률 밀도 함수의 적분으로 계산된다.^[7] 누적 분포 함수는 확률 변수가 주어진 값보다 작거나 같을 확률을 나타내며, 확률 밀도 함수를 음의 무한대부터 해당 값까지 적분한 값과 같다.^[4]

4. 1. 이산 확률 분포

확률 질량 함수를 통해 표현 가능한 이산 확률 분포에는 다음과 같은 예가 있다.

분포	설명
이산균등분포	유한한 수의 모든 가능한 값에 대해 동일한 확률을 가지는 분포이다.
푸아송 분포	단위 시간 또는 단위 공간에서 발생하는 사건의 횟수에 대한 분포이다.
베르누이 분포	성공 또는 실패의 두 가지 결과만을 가지는 시행(베르누이 시행)에 대한 분포이다.
기하 분포	베르누이 시행에서 첫 번째 성공이 나타날 때까지의 시행 횟수에 대한 분포이다.
초기하 분포	비복원 추출에서 특정 속성을 가진 원소의 개수에 대한 분포이다.
이항 분포	독립적인 베르누이 시행을 여러 번 반복했을 때 성공 횟수에 대한 분포이다.
음이항 분포	베르누이 시행에서 특정 횟수의 성공이 나타날 때까지의 시행 횟수에 대한 분포이다.
다항 분포	여러 범주를 가지는 독립적인 시행을 여러 번 반복했을 때 각 범주별 발생 횟수에 대한 분포이다.

이산 확률 분포는 디랙 델타 함수를 사용하여 일반 함수 확률 밀도 함수 ''f'' 로 표현할 수 있다.^[34]

4. 2. 연속 확률 분포 (절대 연속 분포)

'''연속 확률 분포'''(continuous probability distribution^영어)는 확률 밀도 함수를 이용해 분포를 표현할 수 있는 경우를 의미한다. 연속 확률 분포를 가지는 확률변수는 '''연속 확률 변수'''라고 부른다.

확률 변수가 연속체에서 값을 취할 때, 관례적으로 개별 결과에는 확률 0이 할당된다. 이러한 '''연속 확률 변수'''의 경우, 무한히 많은 결과(예: 간격)를 포함하는 사건만 0보다 큰 확률을 갖는다.

절대 연속 확률 분포는 확률 밀도 함수로 설명할 수 있다. 주어진 값의 무한소 확률을 설명하고, 주어진 간격에 결과가 있을 확률은 해당 간격에 대한 확률 밀도 함수를 적분하여 계산할 수 있다.^[7] 분포에 대한 또 다른 설명은 누적 분포 함수를 사용하는 것이다. 이는 확률 변수가 주어진 값보다 크지 않을 확률(즉,

P(X < x)

)을 설명한다. 누적 분포 함수는

-\infty

에서

x

까지의 확률 밀도 함수 아래의 면적이다.^[4]

'''절대 연속 확률 분포'''는 실수선 상의 전체 구간과 같이, 셀 수 없이 많은 가능한 값을 갖는 실수에 대한 확률 분포이며, 여기서 임의의 사건의 확률은 적분으로 표현될 수 있다.^[18] 실수 확률 변수

X

가 함수

f: \Reals \to [0, \infty]

를 갖는다면

X

가 절대 연속 확률 분포를 가지며, 각 구간

I = [a,b] \subset \mathbb{R}

에 대해

X

가

I

에 속할 확률은

I

에 대한

f

의 적분으로 주어진다.^[19]^[20]

:

P\left(a \le X \le b \right) = \int_a^b f(x) \, dx .

이것은 확률 밀도 함수의 정의이므로, 절대 연속 확률 분포는 정확히 확률 밀도 함수를 갖는 확률 분포이다. 특히,

X

가 단일 값

a

를 가질 확률(즉,

a \le X \le a

)은 0이다. 왜냐하면 위아래 한계가 일치하는 적분은 항상 0과 같기 때문이다.

'''절대 연속 확률 변수'''는 확률 분포가 절대 연속인 확률 변수이다.

위에 정의된 절대 연속 확률 분포는 정확히 절대 연속 누적 분포 함수를 갖는 분포이다. 이 경우, 누적 분포 함수

F

는 다음과 같은 형태를 갖는다.

:

F(x) = P(X \leq x) = \int_{-\infty}^x f(t)\,dt

여기서

f

는 분포

P

에 대한 확률 변수

X

의 밀도이다.

자주 사용되는 연속 확률분포에는 다음과 같은 예가 있다.

4. 3. 누적 분포 함수가 연속이지만 절대 연속이 아닌 확률 분포

누적 분포 함수가 연속이지만 절대 연속이 아닌 확률 분포의 예시는 특이 분포이다.

4. 4. 누적 분포 함수가 연속이 아닌 확률 분포

이산 확률 분포의 경우, 확률 밀도 함수에 대응하는 함수로 '''확률 질량 함수'''가 있다. 확률 변수 가 취하는 값의 집합이 라고 하면, 확률 질량 함수는

:

f_X (x_i )=P(X=x_i )=P_X (\{ x_i \} )

로 정의되는 함수 를 말한다. 한국어에서는 '''확률 함수'''로도 줄여서 말하지만, 영어의 'probability function'은 의미가 모호한 단어로 간주된다.

5. 확률 분포의 활용

확률 분포는 표본 공간의 부분 집합인 사건의 확률에 대한 수학적 설명이다. 확률 변수의 분포를 알면 특정 값을 취할 확률, 기댓값, 분산 등을 계산할 수 있다.

예를 들어, "주사위 2개를 던졌을 때 눈의 합"은 확률 변수이다. 이 확률 변수 X에 대한 분포는 다음 표와 같다.

X가 취하는 값	2	3	4	5	6	7	8	9	10	11	12
P(X의 값이 n을 취함)

이산 확률 변수인 경우에는 확률 분포란 확률 변수의 값에 그 확률(확률 질량 함수)을 대응시키는 함수라고 할 수 있다.

"다음에 전화가 걸려올 때까지의 시간"과 같은 연속형 확률 변수의 경우, 확률 변수 값에서의 확률은 모두 0이 되지만, 누적 분포 함수 F_X를 사용하면 분포를 표현할 수 있다. F_X의 도함수 f_X는 확률 밀도 함수라고 불리며, 확률은 적분을 이용하여 다음과 같이 계산할 수 있다.

: $P(a$

5. 1. 확률 계산

확률 변수의 특정 경우에 대한 확률 분포를 정의하기 위해(따라서 표본 공간을 숫자 집합으로 볼 수 있음), '''이산''' 및 '''절대 연속''' 확률 변수를 구별하는 것이 일반적이다. 이산의 경우, 각 가능한 결과에 확률을 할당하는 확률 질량 함수

p

를 지정하는 것으로 충분하다(예: 공정한 주사위를 던질 때 주사위의 점 수에 해당하는 여섯 개의 숫자에서 6까지는 각각

\tfrac{1}{6}

의 확률을 갖는다). 그런 다음 사건의 확률은 해당 사건을 만족하는 모든 결과의 확률의 합으로 정의된다. 예를 들어, "주사위가 짝수를 던지는" 사건의 확률은 다음과 같다.

p(\text{“}2\text{”}) + p(\text{“}4\text{”}) + p(\text{“}6\text{”}) = \tfrac{1}{6} + \tfrac{1}{6} + \tfrac{1}{6} = \tfrac{1}{2}.

반대로, 확률 변수가 연속체에서 값을 취할 때, 관례적으로 개별 결과에는 확률 0이 할당된다. 이러한 '''연속 확률 변수'''의 경우, 무한히 많은 결과(예: 간격)를 포함하는 사건만 0보다 큰 확률을 갖는다.

예를 들어, 슈퍼마켓에서 햄 조각의 무게를 측정하는 것을 고려하고 저울이 임의로 많은 정밀도를 제공할 수 있다고 가정한다. 그러면, 정확히 500g의 무게가 나갈 확률은 0이어야 한다. 왜냐하면 선택된 정밀도가 아무리 높더라도 정밀도 수준에 의해 무시되는 나머지 생략된 숫자에는 0이 아닌 소수 자릿수가 없다고 가정할 수 없기 때문이다.

그러나 동일한 사용 사례의 경우, "500g" 햄 포장이 적어도 98% 확률로 490g에서 510g 사이의 무게가 나가야 한다는 품질 관리 요구 사항을 충족할 수 있다. 이는 이 측정이 기본 장비에서 많은 정밀도를 요구하지 않기 때문이다.

절대 연속 확률 분포는 여러 가지 방법으로 설명할 수 있다. 확률 밀도 함수는 주어진 값의 무한소 확률을 설명하고, 주어진 간격에 결과가 있을 확률은 해당 간격에 대한 확률 밀도 함수를 적분하여 계산할 수 있다.^[7] 분포에 대한 또 다른 설명은 누적 분포 함수를 사용하는 것이다. 이는 확률 변수가 주어진 값보다 크지 않을 확률(즉,

x

에 대한

\mathcal{P}(X < x)

)을 설명한다. 누적 분포 함수는 그림 1에 표시된 것처럼

-\infty

에서

x

까지의 확률 밀도 함수 아래의 면적이다.^[4]

$X$ 가 $a$ 이상 $b$ 이하의 값을 가질 확률
* $P(a \leq X \leq b) = \int_a^b f_X(x) \, dx$
* $P(a \leq X \leq b) = F_X(b) - F_X(a)$
$Y$ 의 값이 집합 $T \subset S$ 에 속할 확률
* $P(Y \in T) = \sum_{y_k \in T} f_Y (y_k)$

5. 2. 기댓값 계산

두 확률 변수 와 의 합 의 확률 분포나 차 의 확률 분포는 변수 변환 공식을 통해 계산할 수 있다. 특히 와 가 독립이고, 확률 밀도 함수가 각각 와 라고 하면, 합과 차의 확률 밀도 함수는 다음과 같다.

:

f_{X+Y} (t) = \int_{-\infty}^{+\infty} f_X (t-y) f_Y (y) \, dy

:

f_{X-Y} (t) = \int_{-\infty}^{+\infty} f_X (t+y) f_Y (y) \, dy

특히 합의 확률 밀도 함수는 두 분포의 확률 밀도 함수의 합성곱이다. 또한, 특성 함수는 확률 밀도 함수의 푸리에 변환이며, 합성곱의 푸리에 변환은 주파수 영역에서의 곱이므로, 합의 특성 함수는 두 분포의 특성 함수의 곱이 된다.

확률 변수의 합의 확률 분포가 원래 분포족을 따르는 경우, 해당 분포는 재생성이 있다고 한다.

5. 3. 분산 계산

확률 변수 ''X''의 분산은 다음과 같이 계산한다.

:

\operatorname{Var}(X) = \operatorname{E}[(X - \operatorname{E}[X])^2]

여기서

\operatorname{E}[X]

는 ''X''의 기댓값(평균)이다.

확률 변수 ''X''와 ''Y''가 있을 때, 이들 합의 분산은 다음과 같이 계산할 수 있다.

:

\operatorname{Var}(X + Y) = \operatorname{Var}(X) + \operatorname{Var}(Y) + 2\operatorname{Cov}(X, Y)

여기서

\operatorname{Cov}(X, Y)

는 ''X''와 ''Y''의 공분산이다. 만약 ''X''와 ''Y''가 서로 독립이면,

\operatorname{Cov}(X, Y) = 0

이므로,

:

\operatorname{Var}(X + Y) = \operatorname{Var}(X) + \operatorname{Var}(Y)

가 된다.

6. 변수 변환

확률 변수를 변환하면 새로운 확률 변수를 얻을 수 있다. 이때, 새로운 확률 변수의 확률 밀도 함수는 원래 확률 변수의 확률 밀도 함수를 이용하여 나타낼 수 있다. 이러한 변수 변환은 컴퓨터를 이용한 난수 생성에서 중요한 역할을 한다.

두 확률 변수의 합이나 차의 확률 분포 또한 변수 변환 공식을 통해 계산할 수 있다. 특히 두 확률 변수가 서로 독립이고 각각의 확률 밀도 함수를 알고 있다면, 합과 차의 확률 밀도 함수를 구할 수 있다.

6. 1. 확률 밀도 함수의 변수 변환 공식

확률 변수의 변수 변환에 따른 새로운 변수의 밀도 함수는, 원래 변수의 밀도 함수로 나타낼 수 있다. 이 공식은 중적분에서의 변수 변환과 거의 유사하다.

\mathbb{R}^d

에서

\mathbb{R}^d

로의 변환 T에 의해,

\mathbb{R}^d

값 확률 변수 X와 Y가

:

X=T(Y)

로 쓰여진다고 하면, Y의 확률 밀도 함수는 X의 확률 밀도 함수를 사용하여

:

f_Y (y_1 , \cdots, y_d ) = |(\det J_T )( y_1 , \cdots , y_d )| f_X (T( y_1 , \cdots , y_d ))

가 된다. 단, J는 야코비안으로 한다.

예를 들어, 박스-뮬러 변환은

(0, 1]^2

상의 균등 분포를 따르는 확률 변수

X = (X_1, X_2)

를

:

Y_1 = \sqrt{-2 \ln X_1} \sin(2\pi X_2)

:

Y_2 = \sqrt{-2 \ln X_1} \cos(2\pi X_2)

에 의해 변환한다. X의 밀도 함수는

:

f_X ( x_1 , x_2 ) = \begin{cases}1, &(x_1 , x_2 ) \in (0, 1]^2 \\0, & (x_1, x_2) \notin (0,1]^2\end{cases}

이며, 위의 공식을 적용하면 Y의 확률 밀도 함수는

:

f_Y ( y_1, y_2 ) = \frac{1}{2\pi} \exp \left( -\frac{{y_1}^2 + {y_2}^2}{2} \right)

가 되어, Y가 이차원 표준 정규 분포를 따른다는 것을 알 수 있다. 이처럼 단순한 분포를 가진 변수를 변환하여 복잡한 분포를 만드는 조작은 컴퓨터에 의한 난수 생성에서 중요해진다.

6. 2. 확률 변수 합의 확률 분포

확률 변수의 변수 변환에 따른 새로운 변수의 밀도 함수는, 원래 변수의 밀도 함수로 나타낼 수 있다. 이 공식은 중적분에서의 변수 변환과 거의 유사하다.

두 확률 변수 ''X''와 ''Y''의 합 ''X'' + ''Y''의 확률 분포나 차 ''X'' - ''Y''의 확률 분포는 변수 변환 공식을 통해 계산할 수 있다. 특히 ''X''와 ''Y''가 독립이고, 확률 밀도 함수가 각각

f_X

와

f_Y

라고 하면, 합과 차의 확률 밀도 함수는 다음과 같다.

:

f_{X+Y} (t) = \int_{-\infty}^{+\infty} f_X (t-y) f_Y (y) \, dy

:

f_{X-Y} (t) = \int_{-\infty}^{+\infty} f_X (t+y) f_Y (y) \, dy

특히 합의 확률 밀도 함수는 두 분포의 확률 밀도 함수의 합성곱이다. 또한, 특성 함수는 확률 밀도 함수의 푸리에 변환이며, 합성곱의 푸리에 변환은 주파수 영역에서의 곱이므로, 합의 특성 함수는 두 분포의 특성 함수의 곱이 된다.

확률 변수의 합의 확률 분포가 원래 분포족을 따르는 경우, 해당 분포는 재생성이 있다고 한다.

7. 확률 모델

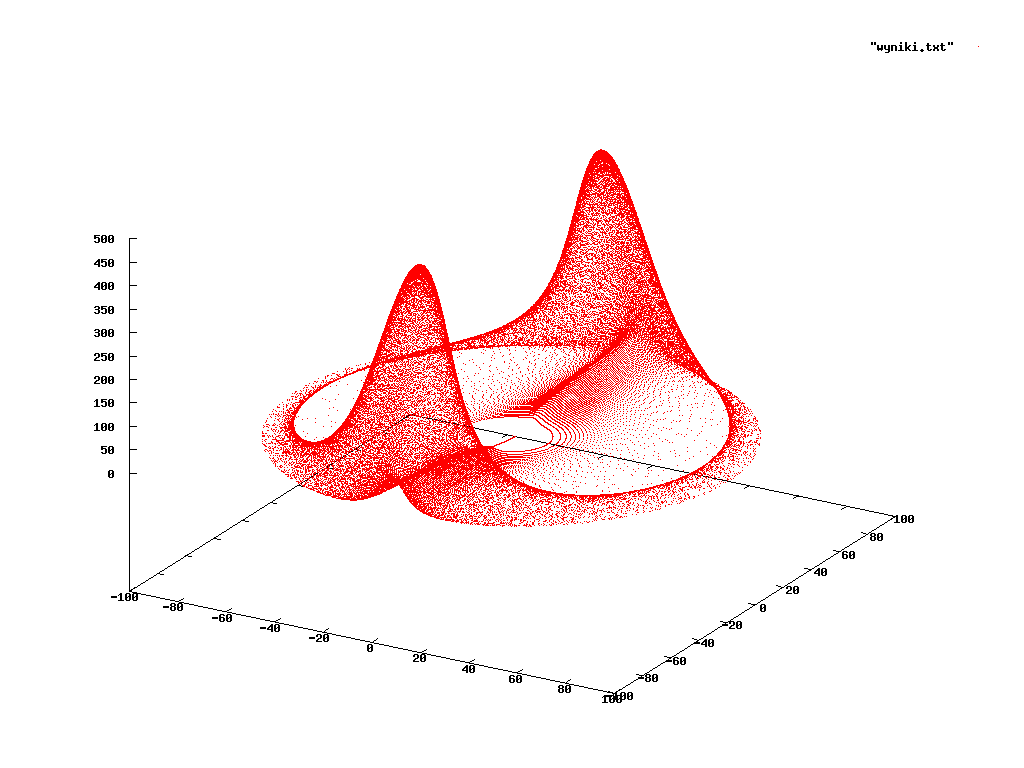
$\mathbb{R}^k$ 또는 $\mathbb{N}^k$ 를 지지체로 하는 절대 연속 및 이산 분포는 수많은 현상을 모델링하는 데 매우 유용하다.^[4] 이는 대부분의 실제 분포가 하이퍼큐브나 구와 같은 비교적 간단한 하위 집합을 지지하기 때문이다. 그러나 항상 그런 것은 아니며, 일부 공간 $\mathbb{R}^n$ 내에서 복잡한 곡선 $\gamma: [a, b] \rightarrow \mathbb{R}^n$ 과 유사한 지지체를 가진 현상도 존재한다. 이러한 경우 확률 분포는 그러한 곡선의 이미지에서 지지되며, 이에 대한 닫힌 공식을 찾는 것보다 경험적으로 결정될 가능성이 높다.^[25]

라비노비치-파브리칸트 방정식(Rabinovich–Fabrikant equations)의 한 가지 해. 지지체의 특정 위치(예: 빨간색 하위 집합)에서 상태를 관찰할 확률은 얼마인가?

오른쪽 그림은 미분 방정식 시스템 (일반적으로 라비노비치-파브리칸트 방정식(Rabinovich–Fabrikant equations)으로 알려짐)의 진화를 보여주는 한 가지 예시이며, 이는 플라즈마에서 랑뮤어파의 동작을 모델링하는 데 사용될 수 있다.^[26] 이 현상을 연구할 때, 하위 집합에서 관찰된 상태는 빨간색으로 표시된 것과 같다. 따라서 빨간색 하위 집합의 특정 위치에서 상태를 관찰할 확률이 무엇인지 질문할 수 있으며, 그러한 확률이 존재한다면 이를 시스템의 확률 측도라고 한다.^[27]^[4]

이러한 종류의 복잡한 지지체는 동역학적 시스템에서 매우 자주 나타난다. 시스템이 확률 측도를 갖는지 확인하는 것은 간단하지 않다.

t_1 \ll t_2 \ll t_3

를 시간의 순간으로,

O

를 지지체의 하위 집합이라고 할 때, 만약 시스템에 대한 확률 측도가 존재한다면 집합

O

내에서 상태를 관찰하는 빈도는 간격

[t_1,t_2]

와

[t_2,t_3]

에서 같을 것으로 예상되지만, 그렇지 않을 수 있다. 예를 들어,

t \rightarrow \infty

일 때 극한이 수렴하지 않는 사인,

\sin(t)

와 유사하게 진동할 수 있다. 형식적으로, 시스템이 무한한 미래로 관찰될 때 상대 빈도의 극한이 수렴하는 경우에만 측도가 존재한다.^[28] 확률 측도의 존재를 연구하는 동역학적 시스템의 분야는 에르고딕 이론이다.

이러한 경우에도, 확률 분포는 지지체가 셀 수 없는지 또는 셀 수 있는지에 따라 각각 "절대 연속" 또는 "이산"으로 불릴 수 있다.

확률 모델은 다양한 분야에서 활용된다. 주요 모델로는 퍼콜레이션, 분기 과정, 랜덤 워크, 무한 입자계, 응집, 모래산 붕괴, 정체, 생명, 배타 과정 등이 있다.

7. 1. 퍼콜레이션

퍼콜레이션 참조. 침투(percolation) 확률에 기초한 모델이다. 구체적으로 산불의 확산, 전염병의 전파, 금속과 절연체의 혼합물, 강자성 원소와 비자성 원소의 혼정계, 분자 간의 중합에 의한 거대 고분자의 겔화 등이 있다.

7. 2. 분기 과정

분기 과정은 생명의 수 변화 모델이다.^[1]

7. 3. 랜덤 워크

랜덤 워크는 무작위적인 움직임을 모델링한다.

7. 4. 무한 입자계

무한 입자의 전이율의 연속 시간 모델이다.^[1]

7. 5. 응집

확산 제한 응집(DLA: diffusion limited aggregation)은 비튼과 선더가 제시한, 입자 클러스터가 응집하여 성장하는 모델이다.^[1]

7. 6. 모래 산 붕괴

백(Bak) 등이 제안한 모래 산의 경사면 붕괴를 나타내는 모델이다.

7. 7. 정체

교통 흐름의 정체 모델이다.

7. 8. 생명

생명은 시간적, 공간적 모델이다. 셀룰러 오토마톤이라고도 부른다. 생명 게임은 2차원 셀룰러 오토마톤의 일종이다.

7. 9. 배타 과정

배타 과정(exclusion process)은 연속 시간으로 발전하는 확률 모델이다. 위의 생명 모델은 이산 시간의 결정론적 모델에 대응한다.^[1]

8. 난수 생성

대부분의 알고리즘은 0과 1 사이의 반열린 구간에 균등하게 분포된 숫자를 생성하는 의사 난수 생성기를 기반으로 한다. 이러한 확률 변수는 필요한 확률 분포를 갖는 새로운 확률 변수를 만들기 위해 변환된다. 균일한 의사 난수를 통해 임의 변수의 실현이 생성될 수 있다.^[29]

예를 들어 $U$ 가 0과 1 사이에서 균일 분포를 갖는다고 가정해 보자. $0 < p < 1$ 에 대한 임의의 베르누이 변수를 구성하기 위해 다음과 같이 정의한다.

: $X = \begin{cases}:1,& \text{if } U:0,& \text{if } U\geq p:\end{cases}$

그래서

: $\Pr(X=1) = \Pr(U\Pr(X=0) = \Pr(U\geq p) = 1-p.$

이 임의 변수 ''X''는 모수 $p$ 를 갖는 베르누이 분포를 갖는다.^[29] 이것은 이산 확률 변수의 변환이다.

절대적으로 연속적인 확률 변수의 분포 함수 $F$ 의 경우, 절대적으로 연속적인 확률 변수를 구성해야 한다. $F$ 의 역함수인 $F^{\mathit{inv}}$ 는 균일 변수 $U$ 와 관련이 있다.

: $\{U\leq F(x)\} = \{F^{\mathit{inv}}(U)\leq x\}.$

예를 들어, 지수 분포 $F(x) = 1 - e^{-\lambda x}$ 를 갖는 확률 변수를 구성해야 한다고 가정해 보자.

: $\begin{align}:F(x) = u &\Leftrightarrow 1-e^{-\lambda x} = u \\[2pt]:&\Leftrightarrow e^{-\lambda x } = 1-u \\[2pt]:&\Leftrightarrow -\lambda x = \ln(1-u) \\[2pt]:&\Leftrightarrow x = \frac{-1}{\lambda}\ln(1-u):\end{align}$

따라서 $F^{\mathit{inv}}(u) = \frac{-1}{\lambda}\ln(1-u)$ 이고 $U$ 가 $U(0,1)$ 분포를 갖는다면, 확률 변수 $X$ 는 $X = F^{\mathit{inv}}(U) = \frac{-1}{\lambda} \ln(1-U)$ 로 정의된다. 이것은 $\lambda$ 의 지수 분포를 갖는다.^[29]

통계적 시뮬레이션 ( 몬테카를로 방법 )의 문제는 주어진 방식으로 분포된 의사 난수를 생성하는 것이다.

9. 일반적인 확률 분포와 응용

확률 분포는 확률 이론과 통계학의 수학적 원리를 기반으로 한다. 사람의 키, 금속의 내구성, 판매 성장, 교통 흐름 등 측정 가능한 거의 모든 값에는 분산 또는 변동이 존재한다. 또한 거의 모든 측정에는 고유한 오차가 수반되며, 물리학의 많은 과정은 기체의 운동 특성부터 양자 역학의 기본 입자 설명에 이르기까지 확률적으로 설명된다. 따라서 단순한 숫자보다는 확률 분포가 양을 설명하는 데 더 적절한 경우가 많다.

다음은 관련 프로세스 유형별로 그룹화된 가장 일반적인 확률 분포의 목록이다. 고려되는 결과의 성격(이산형, 절대 연속형, 다변량 등)별로 그룹화되어 있다.

아래의 모든 단변량 분포는 단봉 분포(값이 단일 지점 주위에 모여 있다고 가정)이다. 실제로는 관찰된 수량이 여러 값 주위에 모일 수 있으며, 이러한 수량은 혼합 분포를 사용하여 모델링할 수 있다.

선형 증가 (예: 오차, 오프셋)

정규 분포: 가장 일반적으로 사용되는 절대 연속 확률 분포이다.^[1]

지수 증가 (예: 가격, 소득, 인구)

로그 정규 분포: 로그 값이 정규 분포를 따르는 경우이다.^[1]

파레토 분포: 로그 값이 지수 분포를 따르는 경우로, 멱법칙 분포의 전형적인 예시이다.^[1]

균등하게 분포된 수량

이산 균등 분포: 유한한 값의 집합에 대한 분포로, 공정한 주사위를 던졌을 때 나오는 결과가 그 예이다.

연속균등분포: 절대적으로 연속적으로 분포된 값에 대한 분포이다.

베르누이 시행 (주어진 확률의 예/아니오 이벤트)

베르누이 분포: 단일 베르누이 시행의 결과 (예: 성공/실패, 예/아니오)에 대한 분포이다.^[1]

이항 분포: 고정된 총 독립 시행 횟수에서 "긍정적인 발생" (예: 성공, 예 투표 등)의 수에 대한 분포이다.^[1]

음이항 분포: 이항 유형의 관찰이지만 관심 있는 양은 주어진 성공 횟수에 도달하기 전의 실패 횟수이다.^[1]

기하 분포: 이항 유형의 관찰이지만 관심 있는 양은 첫 번째 성공 전의 실패 횟수이다. 음이항 분포의 특별한 경우이다.^[1]

유한 모집단에 대한 표본 추출:^[1]

초기하 분포: 비복원 추출을 사용하여 고정된 총 발생 횟수에서 "긍정적인 발생" (예: 성공, 예 투표 등)의 수에 대한 분포이다.^[1]

베타-이항 분포: 폴리야 항아리 모델을 사용하여 표본 추출을 할때, 고정된 총 발생 횟수에서 "긍정적인 발생" (예: 성공, 예 투표 등)의 수에 대한 분포이다. (어떤 의미에서, 비복원 추출의 "반대")^[1]

범주형 결과 (K개의 가능한 결과가 있는 이벤트)

범주형 분포: 단일 범주형 결과(예: 설문 조사에서 예/아니오/아마도)에 대한 분포로, 베르누이 분포의 일반화이다.^[1]

다항 분포: 고정된 총 결과 수에서 각 범주형 결과 유형의 수에 대한 분포로, 이항 분포의 일반화이다.^[1]

다변량 초 기하 분포: 다항 분포와 유사하지만, 비복원 추출을 사용하며, 초 기하 분포의 일반화이다.^[1]

푸아송 과정 (주어진 비율로 독립적으로 발생하는 이벤트)

푸아송 분포: 주어진 시간 동안 푸아송형 사건이 발생하는 횟수에 대한 분포이다.^[1]

지수 분포: 다음 푸아송형 사건이 발생하기까지의 시간에 대한 분포이다.^[1]

감마 분포: 다음 k개의 푸아송형 사건이 발생하기까지의 시간에 대한 분포이다.^[1]

정규 분포된 구성 요소를 갖는 벡터의 절대값

레일리 분포: 정규 분포를 따르는 직교 성분을 가진 벡터 크기의 분포로, 가우스 분포를 따르는 실수 및 허수 성분을 가진 RF 신호에서 발견된다.^[1]

라이스 분포: 고정된 배경 신호 성분이 있는 경우의 레일리 분포를 일반화한 것이다.^[1] 라이스 분포는 다중 경로 전파로 인한 무선 신호의 라이시안 페이딩 및 0이 아닌 NMR 신호에 대한 잡음 손상된 MR 이미지에서 발견된다.^[1]

제곱의 합으로 작동하는 정규 분포 수량

카이제곱 분포: 표준 정규 분포 변수를 제곱하여 합한 분포이다. 예를 들어 정규 분포 표본의 표본 분산에 대한 추론에 유용하며, 카이제곱 검정에 사용된다.^[1]

스튜던트 t-분포: 표준 정규 분포 변수를 스케일링된 카이제곱 분포 변수의 제곱근으로 나눈 비율의 분포이다. 분산을 알 수 없는 정규 분포 표본의 평균에 대한 추론에 유용하며, 스튜던트 t-검정에 사용된다.^[1]

F-분포: 두 개의 스케일링된 카이제곱 분포 변수의 비율의 분포이다. 분산 비교나 R-제곱 (제곱된 피어슨 상관 계수)과 관련된 추론에 유용하다.^[1]

베이즈 추론에서 켤레 사전 분포

베타 분포: 0과 1 사이의 실수인 단일 확률에 사용되며, 베르누이 분포와 이항 분포의 켤레 사전 분포이다.

감마 분포: 음수가 아닌 스케일 매개변수에 사용되며, 푸아송 분포 또는 지수 분포의 비율 매개변수, 정규 분포의 정밀도(역 분산)의 켤레 사전 분포이다.

디리클레 분포: 합이 1이 되어야 하는 확률 벡터에 사용되며, 범주형 분포 및 다항 분포의 켤레 사전 분포이고, 베타 분포의 일반화이다.

위샤트 분포: 대칭 반정부호 행렬에 사용되며, 다변량 정규 분포의 공분산 행렬의 역수의 켤레 사전 분포이고, 감마 분포의 일반화이다.

확률 분포의 일부 특수 응용

캐시 언어 모델 및 자연어 처리에 사용되는 다른 통계적 언어 모델은 특정 단어와 단어 시퀀스의 발생 확률을 할당하기 위해 확률 분포를 사용한다.

양자역학에서 주어진 지점에서 입자를 발견할 확률 밀도는 해당 지점에서 입자의 파동 함수 크기의 제곱에 비례한다(본 규칙 참조). 따라서 입자 위치의 확률 분포 함수는

P_{a\le x\le b} (t) = \int_a^b d x\,|\Psi(x,t)|^2

로 설명되며, 이는 입자가 1차원 구간

[a,b]

에 있을 확률과 3차원에서의 유사한 삼중 적분을 나타낸다. 이것은 양자역학의 핵심 원리이다.^[31]

전력 조류 계산에서 확률적 부하 흐름은 입력 변수의 불확실성을 확률 분포로 설명하고 확률 분포 측면에서 전력 흐름 계산을 제공한다.^[32]

열대성 저기압, 우박, 사건 간의 시간 등과 같은 이전 빈도 분포를 기반으로 자연 현상 발생을 예측한다.^[33]

9. 1. 선형 증가 (예: 오차, 오프셋)

정규 분포는 가장 일반적으로 사용되는 절대 연속 확률 분포이다.^[1]

9. 2. 지수 증가 (예: 가격, 소득, 인구)

로그 정규 분포는 로그 값이 정규 분포를 따르는 경우이고, 파레토 분포는 로그 값이 지수 분포를 따르는 경우로, 멱법칙 분포의 전형적인 예시이다.^[1]

9. 3. 균등하게 분포된 수량

이산 균등 분포는 유한한 값의 집합에 대한 분포로, 공정한 주사위를 던졌을 때 나오는 결과가 그 예이다.
연속균등분포는 절대적으로 연속적으로 분포된 값에 대한 분포이다.

9. 4. 베르누이 시행 (주어진 확률의 예/아니오 이벤트)

베르누이 분포: 단일 베르누이 시행의 결과 (예: 성공/실패, 예/아니오)^[1]

이항 분포: 고정된 총 독립 시행 횟수에서 "긍정적인 발생" (예: 성공, 예 투표 등)의 수^[1]

음이항 분포: 이항 유형의 관찰이지만 관심 있는 양은 주어진 성공 횟수에 도달하기 전의 실패 횟수^[1]

기하 분포: 이항 유형의 관찰이지만 관심 있는 양은 첫 번째 성공 전의 실패 횟수. 음이항 분포의 특별한 경우^[1]

유한 모집단에 대한 표본 추출 방식:^[1]

초기하 분포: 비복원 추출을 사용하여 고정된 총 발생 횟수에서 "긍정적인 발생" (예: 성공, 예 투표 등)의 수^[1]
베타-이항 분포: 폴리야 항아리 모델을 사용하여 표본 추출을 할때, 고정된 총 발생 횟수에서 "긍정적인 발생" (예: 성공, 예 투표 등)의 수 (어떤 의미에서, 비복원 추출의 "반대")^[1]

9. 5. 범주형 결과 (K개의 가능한 결과가 있는 이벤트)

범주형 분포는 단일 범주형 결과(예: 설문 조사에서 예/아니오/아마도)에 대한 분포로, 베르누이 분포의 일반화이다.^[1] 다항 분포는 고정된 총 결과 수에서 각 범주형 결과 유형의 수에 대한 분포로, 이항 분포의 일반화이다.^[1] 다변량 초 기하 분포는 다항 분포와 유사하지만, 비복원 추출을 사용하며, 초 기하 분포의 일반화이다.^[1]

9. 6. 푸아송 과정 (주어진 비율로 독립적으로 발생하는 이벤트)

푸아송 분포는 주어진 시간 동안 푸아송형 사건이 발생하는 횟수에 대한 분포이다.^[1] 지수 분포는 다음 푸아송형 사건이 발생하기까지의 시간에 대한 분포이다.^[1] 감마 분포는 다음 k개의 푸아송형 사건이 발생하기까지의 시간에 대한 분포이다.^[1]

9. 7. 정규 분포된 구성 요소를 갖는 벡터의 절대값

레일리 분포는 정규 분포를 따르는 직교 성분을 가진 벡터 크기의 분포로, 가우스 분포를 따르는 실수 및 허수 성분을 가진 RF 신호에서 발견된다.^[1] 라이스 분포는 고정된 배경 신호 성분이 있는 경우의 레일리 분포를 일반화한 것이다.^[1] 라이스 분포는 다중 경로 전파로 인한 무선 신호의 라이시안 페이딩 및 0이 아닌 NMR 신호에 대한 잡음 손상된 MR 이미지에서 발견된다.^[1]

9. 8. 제곱의 합으로 작동하는 정규 분포 수량

카이제곱 분포는 표준 정규 분포 변수를 제곱하여 합한 분포이다. 예를 들어 정규 분포 표본의 표본 분산에 대한 추론에 유용하며, 카이제곱 검정에 사용된다.^[1]

스튜던트 t-분포는 표준 정규 분포 변수를 스케일링된 카이제곱 분포 변수의 제곱근으로 나눈 비율의 분포이다. 분산을 알 수 없는 정규 분포 표본의 평균에 대한 추론에 유용하며, 스튜던트 t-검정에 사용된다.^[1]

F-분포는 두 개의 스케일링된 카이제곱 분포 변수의 비율의 분포이다. 분산 비교나 R-제곱 (제곱된 피어슨 상관 계수)과 관련된 추론에 유용하다.^[1]

9. 9. 베이즈 추론에서 켤레 사전 분포로

베타 분포는 0과 1 사이의 실수인 단일 확률에 사용되며, 베르누이 분포와 이항 분포의 켤레 사전 분포이다.
감마 분포는 음수가 아닌 스케일 매개변수에 사용되며, 푸아송 분포 또는 지수 분포의 비율 매개변수, 정규 분포의 정밀도(역 분산)의 켤레 사전 분포이다.
디리클레 분포는 합이 1이 되어야 하는 확률 벡터에 사용되며, 범주형 분포 및 다항 분포의 켤레 사전 분포이고, 베타 분포의 일반화이다.
위샤트 분포는 대칭 반정부호 행렬에 사용되며, 다변량 정규 분포의 공분산 행렬의 역수의 켤레 사전 분포이고, 감마 분포의 일반화이다.

9. 10. 확률 분포의 일부 특수 응용

캐시 언어 모델 및 자연어 처리에 사용되는 다른 통계적 언어 모델은 특정 단어와 단어 시퀀스의 발생 확률을 할당하기 위해 확률 분포를 사용한다.
양자역학에서 주어진 지점에서 입자를 발견할 확률 밀도는 해당 지점에서 입자의 파동 함수 크기의 제곱에 비례한다(본 규칙 참조). 따라서 입자 위치의 확률 분포 함수는 $P_{a\le x\le b} (t) = \int_a^b d x\,|\Psi(x,t)|^2$ 로 설명되며, 이는 입자 위치 가 1차원 구간 에 있을 확률과 3차원에서의 유사한 삼중 적분을 나타낸다. 이것은 양자역학의 핵심 원리이다.^[31]
전력 조류 계산에서 확률적 부하 흐름은 입력 변수의 불확실성을 확률 분포로 설명하고 확률 분포 측면에서 전력 흐름 계산을 제공한다.^[32]
열대성 저기압, 우박, 사건 간의 시간 등과 같은 이전 빈도 분포를 기반으로 자연 현상 발생을 예측한다.^[33]

10. 적합

확률 분포 적합은 관측된 데이터에 가장 잘 맞는 확률 분포를 찾는 과정이다. 이는 데이터의 특성을 이해하고, 미래의 사건을 예측하며, 다양한 통계적 분석을 수행하는 데 필수적이다.

참조

_[1] 서적 The Cambridge dictionary of statistics Cambridge University Press 2006
_[2] 서적 Basic probability theory Dover Publications 2008
_[3] 서적 Probability and statistics: the science of uncertainty W.H. Freeman and Co 2010
_[4] 서적 A Modern Introduction to Probability and Statistics : Understanding why and how Springer 2005
_[5] 서적 Probability and statistics for engineers Prentice Hall
_[6] 서적 Probability and measure Wiley
_[7] 웹사이트 1.3.6.1. What is a Probability Distribution https://www.itl.nist[...] 2020-09-10
_[8] 서적 Probability and Statistics Addison-Wesley
_[9] 간행물 From characteristic function to distribution function: a simple framework for the theory https://ora.ox.ac.uk[...]
_[10] 서적 Vapnik 1998
_[11] 문서 More information and examples can be found in the articles Heavy-tailed distribution, Long-tailed distribution, fat-tailed distribution
_[12] 서적 Probability and stochastics Springer 2011
_[13] 문서 see Lebesgue's decomposition theorem
_[14] 서적 Probability and stochastics Springer 2011
_[15] 서적 Measure theory Birkhäuser 1993
_[16] 간행물 Applications of Dirac's delta function in statistics 2004-03
_[17] 서적 Probability Theory and Mathematical Statistics John Wiley & Sons
_[18] 서적 A First Look at Rigorous Probability Theory World Scientific 2000
_[19] 서적 DeGroot, Schervish 2002
_[20] 웹사이트 11. Probability Distributions - Concepts https://www.intmath.[...] 2020-09-10
_[21] 서적 A first course in probability Pearson
_[22] 서적 Probability theory : an analytic view Cambridge University Press 1999
_[23] 서적 Foundations of the theory of probability Chelsea Publishing Company
_[24] 웹사이트 Axioms of Probability https://mathcs.clark[...] 2014
_[25] 서적 Chaos: an introduction to dynamical systems Springer
_[26] 간행물 Stochastic self-modulation of waves in nonequilibrium media
_[27] 서적 A second course in probability http://people.bu.edu[...]
_[28] 서적 An Introduction to Ergodic Theory Springer
_[29] 서적 Why probability and statistics? Springer London 2005
_[30] 서적 Pattern recognition and machine learning Springer 2006
_[31] 서적 Physical chemistry for the chemical sciences
_[32] 서적 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies 2008-04
_[33] 서적 Statistical methods in hydrology and hydroclimatology 2018-04-30
_[34] 문서 標本点あるいは結果 (確率論)のこと
_[35] 서적 Probability Theory: A Comprehensive Course Springer

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com